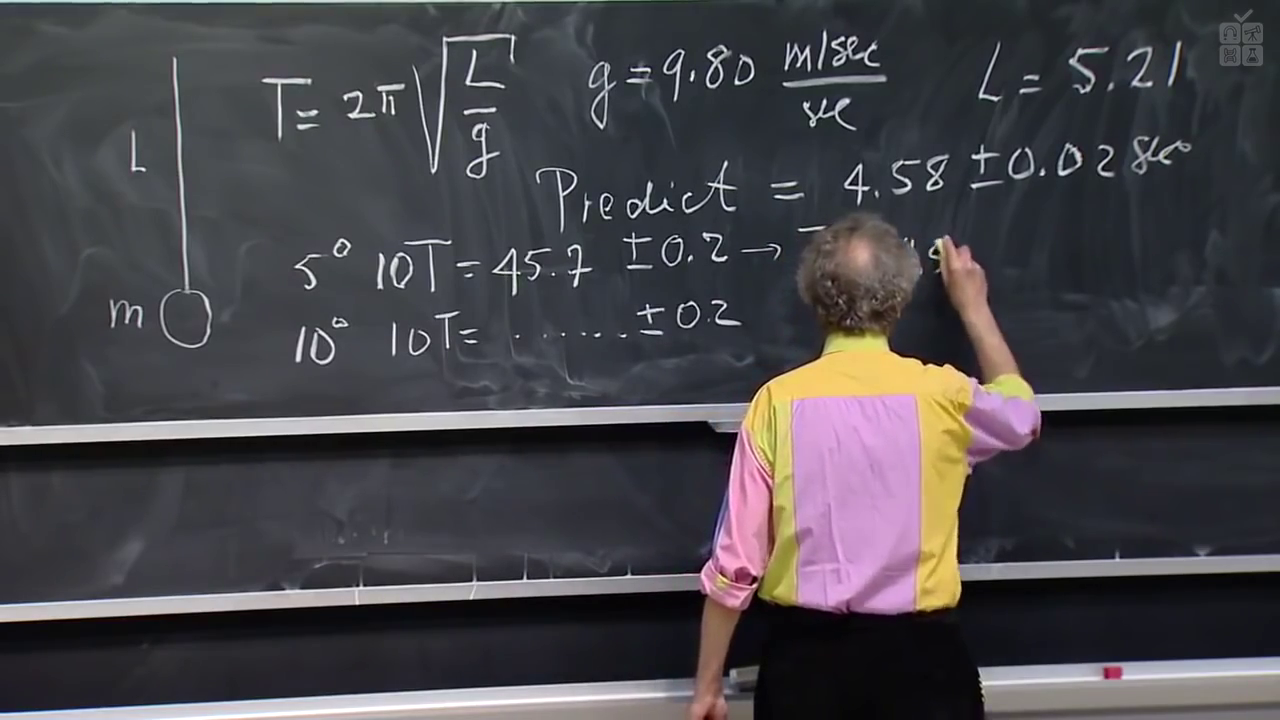Более 30 лет Уолтер Левин преподавал в Массачусетском технологическом институте. Левин на лекциях мог пропустить через собственное тело электрический заряд в 300000 вольт, привязать к ногам весы для выяснения точной массы тела в разном положении и палить из винтовки по банкам из-под краски, чтобы доказать свою теорию.
С помощью этих, на первый взгляд, странных поступков, Левин помогает своим студентам искренне полюбить физику и законы науки. Это же делает и книга «Глазами физика».
Ошибка Галилея
Я решил проверить предположение великого Галилео Галилея, отца современной естественной науки и астрономии, который когда-то задался вопросом: «Почему самые крупные млекопитающие именно такого размера, а не намного больше?», от чего получаю море удовольствия. Сам Галилей полагал, что чересчур крупное млекопитающее было бы слишком тяжелым и его кости не выдержали бы веса и сломались. Когда я об этом прочитал, меня чрезвычайно заинтересовало, прав ли великий ученый. На интуитивном уровне его ответ казался верным, но я все же захотел проверить.
Я знал, что у млекопитающих львиная доля веса приходится на бедренные кости, и решил провести сравнительные замеры бедренных костей разных животных. Если Галилей прав, то бедренные кости супертяжелых млекопитающих будут недостаточно крепкими для поддержания их огромного веса. Конечно, я понимал, что крепость бедренной кости животного зависит от ее толщины. Более толстые кости могут поддерживать больший вес — это понятно на интуитивном уровне. Чем крупнее животное, тем толще должны быть кости.
Кроме того, очевидно, что чем больше размеры животного, тем длиннее его бедренная кость. Я понял, что смогу проверить идею Галилея, сравнивая длину и толщину бедренных костей млекопитающих разного размера и, соответственно, разного веса. На основании произведенных мной расчетов, я пришел к выводу, что если Галилей прав, то толщина бедренных костей млекопитающих по мере увеличения их размеров должна расти быстрее, чем их длина. Я, например, подсчитал, что если одно животное в пять раз больше другого — и, соответственно, его бедренная кость в пять раз длиннее, — то эта кость должна быть примерно в одиннадцать раз толще.
А это означало бы, что в какой-то момент толщина бедренных костей сравнялась бы с их длиной, а то и превысила бы ее, что закономерно сделало бы тело млекопитающего непропорциональным и слишком неуклюжим. Такое животное, конечно же, не имело бы шансов на выживание, чем, скорее всего, и объясняется ограничение максимального размера существующих млекопитающих.
Словом, мое предположение, что толщина кости должна увеличиваться быстрее ее длины. Тут-то и началось самое интересное. Я отправился в Гарвардский университет, где хранится прекрасная коллекция костей животных, и попросил показать мне бедренную кость енота и лошади. Оказывается, лошадь примерно в четыре раза больше енота, и, соответственно, ее бедренная кость (42,0 ± 0,5 см) почти в три с половиной раза больше кости енота (12,4 ± 0,3 см). Пока все шло как надо. Подставив эти числа в свою формулу, я рассчитал, что бедренная кость лошади должна быть примерно в шесть раз толще кости енота. Я измерил толщину костей (с погрешностью около 0,5 сантиметра для енота и 2 сантиметра для лошади) и выяснил, что лошадиная кость в пять раз толще, плюс-минус около 10 процентов. Пока все говорило в пользу теории Галилео Галилея. Однако я решил расширить тест, включив в него более мелких и более крупных млекопитающих.
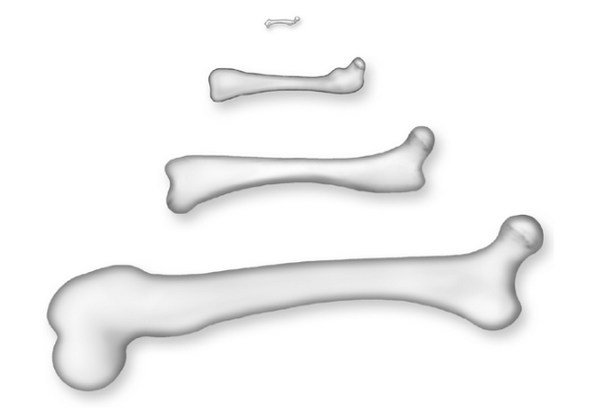
Я опять отправился в Гарвард, где мне показали еще три кости: антилопы, опоссума и мыши. Вот как они выглядели (плюс кость лошади):
Ну разве это не прекрасно? Форма костей изменяется на удивление пропорционально; вы только поглядите, какая тоненькая и крошечная бедренная кость мыши! Малюсенькая и тонюсенькая бедренная косточка для малюсенькой мышки. Разве это не замечательно? Никогда не перестану поражаться красоте каждой детали матушки-природы.
Но как насчет результатов измерений, как они вписываются в мое уравнение? Произведенные расчеты повергли меня в шок, настоящий шок. Бедренная кость лошади оказалась примерно в 40 раз длиннее кости мыши и, согласно моим расчетам, в этом случае должна была быть более чем в 250 раз толще. А она была толще всего примерно в 70 раз.
И тут меня осенило: «А почему бы не попросить у них бедренную кость слона? Это помогло бы окончательно решить вопрос». Думаю, ребята в Гарварде были несколько раздражены, когда я явился к ним снова, но все же любезно выдали мне бедренную кость слона. К тому времени, я уверен, они просто хотели поскорее от меня избавиться! Поверьте, кость слона было очень трудно нести; она была длиннющая и, похоже, весила целую тонну. Я не мог дождаться момента, когда ее измерю, и не спал всю ночь.
И знаете, что я обнаружил? Бедренная кость мыши была 1,1 ± 0,05 см в длину и всего 0,7 ± 0,1 мм толщиной — действительно очень тонкая. Длина бедренной кости слона составляла 101 ± 1 см, то есть приблизительно в 100 раз длиннее кости мыши. А как насчет толщины? Измерив кость слона, я получил толщину 86 ± 4 мм, то есть примерно в 120 раз больше диаметра бедренной кости
мыши. Однако, по моим расчетам, если Галилей прав, то бедренная кость слона должна была быть где-то в тысячу раз толще, чем у мыши. Иными словами, ее толщина должна составлять около 70 сантиметров. А на самом деле ее диаметр был где-то 9 сантиметров. В итоге мне пришлось признать, хоть и с крайней неохотой, что великий Галилео Галилей ошибался!
Винтовка и банки из-под краски
Для одной из моих любимых демонстраций я приношу в аудиторию две банки из-под краски и винтовку. Затем заполняю одну банку до краев водой и плотно закрываю крышкой, потом заполняю вторую банку, но не до конца, на пару сантиметров ниже края, и тоже плотно закрываю. Поставив их на столе одну за другой, я подхожу ко второму столу, находящемуся в нескольких метрах от первого, на котором стоит длинный белый деревянный ящик с загадочным содержимым. Я открываю крышку, и все видят винтовку, закрепленную на подставке и нацеленную на банки. Глаза студентов расширяются: неужели я собираюсь палить из винтовки в аудитории?
«Что бы было, если бы мы выстрелили в эти банки?» — спрашиваю я их и, не дожидаясь ответа, наклоняюсь, чтобы проверить, правильно ли нацелено оружие, и обычно немного вожусь с затвором. Это весьма эффективно повышает градус напряженности аудитории. Я сдуваю пыль с патронника, вставляю в него пулю и объявляю: «Итак, пуля на месте. Готовы?» Затем кладу палец на спусковой крючок и считаю: «Три, два, один…» — выстрел. Крышка с одной банки мгновенно взлетает в воздух, а на другой остается на месте. И как думаете, с какой банки слетает крышка?
Чтобы ответить на этот вопрос, надо помнить о том, что воздух — вещество сжимаемое, а вода нет; молекулы воздуха могут сдвигаться ближе по направлению друг к другу, как и молекулы любого газа, а молекулы воды не могут, как и молекулы любой жидкости. Чтобы изменить плотность жидкости, необходимо приложить поистине огромную силу и давление. Когда пуля ударяет в банки, она оказывает на них существенное давление. В банке, где есть воздух, вода остается нетронутой, поскольку он действует как подушка, или амортизатор, и банка не взрывается. Но в банке, заполненной водой до краев, вода не может сжаться. Из-за дополнительного давления, возникающего вследствие удара пули, вода сильно давит на стенки и верхнюю часть банки и крышка слетает. В целом все это выглядит очень драматично, и мои студенты обычно находятся под большим впечатлением от данного эксперимента.
Бабушкина теория
Когда какая-то теория не подтверждается фактами, я вспоминаю свою бабушку, мамину маму, поистине великую женщину, которая имела в запасе множество замечательных поговорок и привычек, делавших ее, по сути, на редкость интуитивным ученым. Например, она часто говорила, что стоящий человек короче, чем лежащий. Я обожаю рассказывать об этом своим студентам. В первый же день занятий я объявляю им, что в память о своей бабушке намерен сейчас же проверить эту диковинную идею. Они, конечно же, полностью сбиты с толку. Я буквально читаю их мысли: «Стоя короче, чем лежа? Но это невозможно!»
Для проведения эксперимента мне в первую очередь необходимо убедить аудиторию в точности моих измерений. Поэтому я начинаю с измерения вертикально установленного алюминиевого стержня — его длина составляет 150,0 сантиметров — и прошу слушателей подтвердить, что я определенно способен измерить его с точностью до миллиметра. Итак, длина стержня в вертикальном положении 150,0 ± 0,1 см. Затем я измеряю его в горизонтальном положении и получаю 149,9 ± 0,1 см, что вполне согласуется — с учетом погрешности измерений — с результатом замера в вертикальном положении.

Когда мы ложимся, наш позвоночник расправляется. Источник.
Затем я приглашаю добровольца из зала, измеряю его в стоячем положении и записываю число на доске — скажем, 185,2 см, конечно же, плюс-минус миллиметр с учетом погрешности. Потом помогаю парню улечься на мой стол, оснащенный специальным измерительным прибором, похожим на гигантскую деревянную мерку, которой пользуются обувщики; только я измеряю не ступню, а все тело. Попутно я отпускаю разные шуточки по поводу того, удобно ли добровольцу, шумно благодарю его за то, что он пошел на такую жертву ради науки, и так далее, в результате чего ему становится немного не по себе. Его мучает вопрос, что же я задумал? Я плотно прижимаю треугольный деревянный брусок к макушке парня, лежащего на столе, и пишу на доске второе число. Таким образом, у нас теперь есть два результата измерения, каждое с погрешностью в 1 мм. Итак, что же мы имеем?
Вы наверняка немало удивитесь, услышав, что полученные значения отличаются друг от друга примерно на 2,5 сантиметра, конечно, плюс-минус еще 2 миллиметра. Мне приходится сделать вывод, что мой подопечный действительно как минимум на 2,3 сантиметра выше в лежачем положении, чем в стоячем. Я возвращаюсь к лежащему на столе студенту, объявляю ему, что лежа он примерно на два с половиной сантиметра выше, чем стоя, и — это моя любимая часть — громко провозглашаю: «Моя бабушка была права! Она всегда оказывалась права!»
Вы по-прежнему настроены скептически? Что ж, получается, моя бабушка была проницательнее вас? Когда мы стоим, сила земного тяготения сдавливает мягкие ткани между позвонками нашего позвоночника, а когда ложимся, позвоночник расправляется. Если об этом знаешь, ситуация кажется очевидной, но многие ли об этом задумываются? На самом деле этот эффект не учли даже ученые из НАСА при подготовке первых полетов человека в космос. Астронавты жаловались, что их скафандры в космосе становились слишком тесными. Специальные исследования, проведенные позже, уже во время миссии Скайлэб, показали, что из шести измеренных астронавтов все шестеро в состоянии невесомости оказались примерно на 3 процента выше — при росте 182 сантиметра на 5,8 сантиметра. Теперь скафандры делают немного больше, с учетом этой особенности.
По материалам книги «Глазами физика».