Красота не просто рабочая функциональность и приятная глазу оболочка, но и нечто гораздо большее. По-настоящему красивые вещи не только приносят радость — они намного удобнее в использовании. Но давайте оторвемся от мира вещей и посмотрим на красоту шире. А поможет нам книга «Загмайстер и Уолш: О Красоте».
Красота как идеал
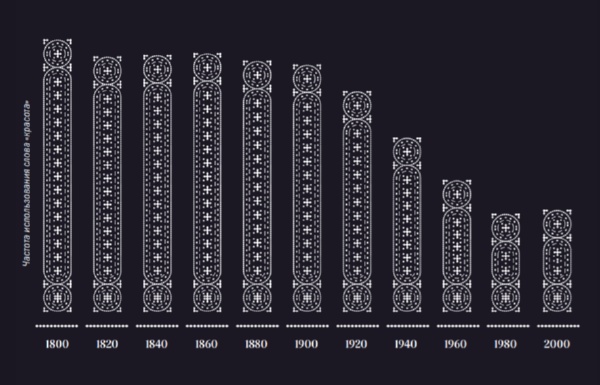
Красота как высший эстетический идеал впала в немилость. Самые уважаемые представители сферы современного дизайна утверждают, что ею не интересуются. Художники избегают ее, опасаясь, что их работы причислят к декоративному или коммерческому искусству. Можно пролистать целую стопку книг по архитектуре и ни разу не встретить даже упоминания слова «красота». Когда-то к ней стремились все, но в начале XX века этот высокий идеал разбился вдребезги.

Загмайстер и Уолш: О Красоте
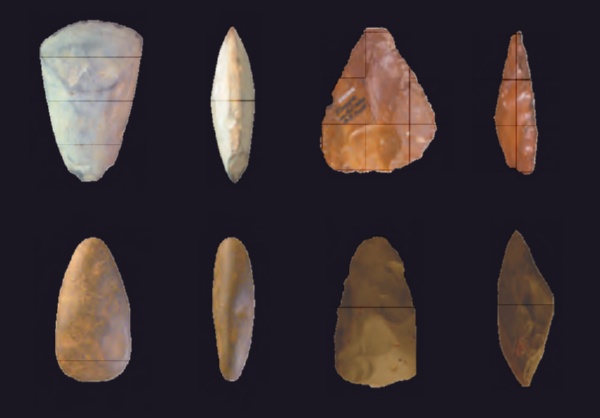
Топоры
Первым орудием человека были каменные топоры. Человек использовал каменный топор еще до появления языка и полной эволюции в разумное человеческое существо (вид Homo sapiens возник лишь около двухсот тысяч лет тому назад).
Но что удивительно, многие каменные топоры идеально симметричны. С точки зрения функциональности в этом нет никакого смысла: саблезубого тигра можно убить и несимметричным заостренным камнем. По мнению философа Дениса Даттона, люди обтачивали камни и придавали им симметрию из эстетических соображений: попросту потому, что им так больше нравилось.
Математическая красота
Американский философ Денис Даттон утверждает, что любое качественно выполненное действие человека можно назвать красивым. Красивый гол в футболе, красивая музыкальная композиция — мы восхищаемся и тем и другим, если это выполнено на высочайшем уровне.
Такое утверждение справедливо даже для математических уравнений. Если формула верна, ее тоже можно назвать изящной и красивой. Об этом говорил лауреат Нобелевской премии по физике Ричард Фейнман: «В правде всегда есть красота и простота, так ее можно отличить от неправды».
Формула красоты
Американский математик Джордж Дэвид Биркхоф пошел еще дальше и в начале XX века создал формулу красоты: мера красоты (М) равна отношению организации (О) к сложности (C).
M=O/С
Он считал, что красота существует где-то между порядком и хаосом и в подтверждение своей теории приводил примеры из мира природы: система ветвей дерева, молния. Представление о зыбком балансе между организацией и сложностью применимо и к творениям рук человеческих. Будь то дизайн ювелирных украшений или план целого города, соблюдение равновесия приводит к красоте, считал Биркхоф.
Природа или человек
Немецкий философ Георг Вильгельм Фридрих Гегель считал, что красоту способен создать только художник, а в природе красоты нет. Да, мы можем считать поле одуванчиков красивым, но картина, изображающая поле одуванчиков, — высшая форма красоты, эстетический триумф, более понятный интеллекту.
Манхэттен
Стефан Загмайстер, один из авторов этой книги, считает, что если сравнить прежний облик Манна-хаты (а именно так назывался Манхэттен, когда Петер Минёйт купил его у населявших остров коренных американцев) и современный Манхэттен, мы увидим, что человеческое вмешательство существенно улучшило это место: теперь остров выглядит гораздо красивее.
Природе понадобилось тридцать миллионов лет, чтобы создать австрийские Альпы, а у ньюйоркцев на создание городского пейзажа Манхэттена ушло всего тридцать. Учитывая скорость развития мегаполиса по сравнению с Альпами, Стефан считает, что нужно отдать должное ньюйоркцам: их достижения впечатляют гораздо больше, чем работа, проделанная природой.

Фракталы
В 1975 году математик Бенуа Мандельброт доказал, что формы, которые мы считаем абсолютно беспорядочными, лишенными структуры, — например, береговые линии, облака, — на самом деле упорядочены. Он сумел воссоздать сложный рисунок береговой линии, следуя простым правилам. Эти структуры он назвал фракталами.
Фракталы определяют форму гор и рек, строение растений и животных, звуки дождя и водопада и являются частью логичной математической последовательности. Человек отдает предпочтение изображениям с фрактальной размерностью от 1,3 до 1,5 независимо от того, созданы ли они природой (побережья, облака), художниками (картины Джексона Поллока) или математиками. Нам нравится вполне определенная степень сложности. Есть даже научные данные, подтверждающие, что созерцание фракталов снижает стресс.
Подготовлено по бестселлеру «Загмайстер и Уолш: О Красоте».
Все иллюстрации — из книги.













