Львиная доля основ математики, которую мы изучаем за школьные годы, — это всего около двух веков ее истории. Причем 3 + 3 для нас слишком легко, а комплексные числа — архисложно. Профессор Иэн Стюарт сделал невероятное. Он собрал под одну обложку 4000 лет математики, от глиняных табличек до теории хаоса, и рассказал об этом легко и понятно.
Портреты и биографии знаменитых ученых всех эпох, наглядное объяснение теорий и открытий, а также их прикладное применение в современной жизни — это и есть наша математическая новинка «Укрощение бесконечности».
Ключи к природе
Сегодня мы принимаем как должное то, что математика дает нам ключи к законам существования природы. Первые же записи об этом пришли от пифагорейцев. Самым важным аспектом их философии была идея, что в основе всего лежат числа.

В мистическом плане они считали, что число 1 — первичный источник всего во Вселенной. Числа 2 и 3 символизируют женское и мужское начала. Число 4 — символ гармонии и четырех стихий (земля, воздух, огонь и вода), из которых сотворено всё сущее. Особое значение было у числа 10, потому что 10 = 1 + 2 + 3 + 4 и объединяет в себе первичную единицу, женское начало, мужское начало и четыре стихии. Более того, эти числа образуют треугольник, а вся геометрия Древней Греции построена на свойствах треугольников.
Лента Мёбиуса и бутылка Клейна
Топология щедра на сюрпризы. Самый известный из них — лента Мёбиуса. Чтобы ее получить, нужно взять длинную полоску бумаги и склеить противоположные концы, повернув один из них вполоборота. Без поворота мы получим обычный цилиндр.

Из-за полуоборота внутренняя поверхность соединилась с наружной. Источник.
Клейн пошел дальше, концептуально склеив в круглый диск края ленты Мёбиуса, чтобы избавиться от края. Получившуюся поверхность в шутку прозвали бутылкой Клейна.
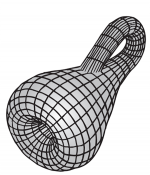
Если мы попытаемся изобразить ее в привычном трехмерном пространстве, ей придется пройти себя насквозь. Но в качестве абстрактной поверхности (или поверхности, помещенной в четырехмерное пространство) она не пронзит себя. Видимое самопересечение — не более чем иллюзия, возникающая из-за трехмерности изображения.
Математика и узоры на шкурах
Теория групп привела к более абстрактному взгляду на математику. В наше время она применяется, в частности, в теории формирования узоров в самых разных отраслях науки. Одним из примеров может быть модель, предложенная Аланом Тьюрингом как одно из возможных объяснений появления пятен на шкурах животных. В уравнениях набор химических веществ может создать диффузию в некоторой области пространства, и эти вещества также вступают в реакции, производя новые.

Математические модели приближаются к сложным генетическим процессам. Источник.
Этот процесс называется деформацией, нарушающей симметрию. Типичный узор, нарушающий симметрию на плоскости, состоит из параллельных полос. Еще один — повторяющиеся наборы пятен. Любопытно, что полосы и пятна — типичные узоры на шкурах животных.
Странный Перельман
В 2002 г. Григорий Перельман произвел сенсацию, выложив несколько своих статей на arXiv — сайте, созданном учеными для нерецензируемых публикаций. Стало понятно, что если открытия автора верны, они послужат доказательством гипотезы Пуанкаре, которая была включена в список восьми математических задач тысячелетия. За их решение можно получить приз в миллион долларов.
Поэтому ученый даже не хотел расшифровать свои малопонятные наброски в нечто более достойное публикации. Эксперты были вынуждены предлагать свои версии развития его идеи. В итоге они добились результата, приемлемого в качестве доказательства, и в 2006 г. Перельману присудили медаль Филдса. Но и от этого приза ученый отказался.
Игры разума
То, что еще вчера казалось не более чем отвлеченными играми разума, завтра может запросто стать жизненно важной областью науки. Читайте в книге:
— когда и как зародилась математика,
— биографии целого пантеона знаменитых мыслителей и их открытия,
— обзор большинства важнейших дисциплин математической науки,
— прикладное значение каждой теории
…и еще 448 страниц увлекательного укрощения бесконечности.
История математики — длинная и причудливая. Первопроходцы в этой науке то совершали гениальные прорывы, то устремлялись по ложным тропам, забредая в тупики, из которых подчас не могли выбраться веками. Но такова судьба любых людей, пытающихся освоить неизведанное.
Четыре тысячи лет математика неизменно черпала вдохновение из двух источников: реального мира и человеческого воображения. Какой из них важнее? Никакой. Для математики имеет значение только их сочетание. Она черпает мощь и красоту равным образом из обоих источников.